Paperwatch 11.06.2025 by Stanislav Fedotov (Nebius Academy)
New Models, Services, and Frameworks
OpenAI o3-pro
https://help.openai.com/en/articles/9624314-model-release-notes
o3-pro is a new reasoner from OpenAI, which is allegedly not actually a new model, but rather an agent on top of o3, designed to think longer and provide the most reliable responses.
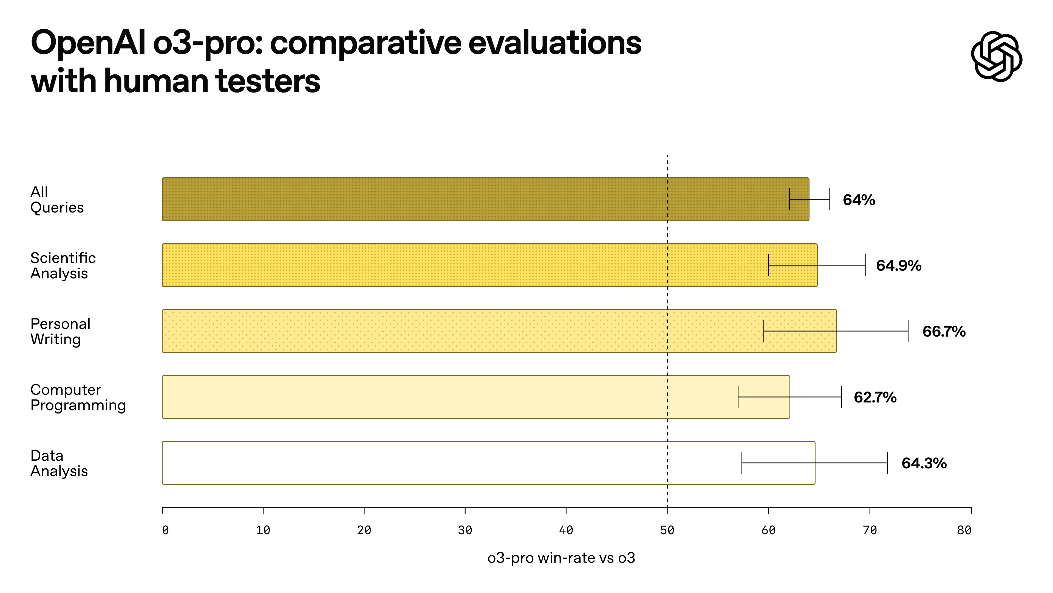
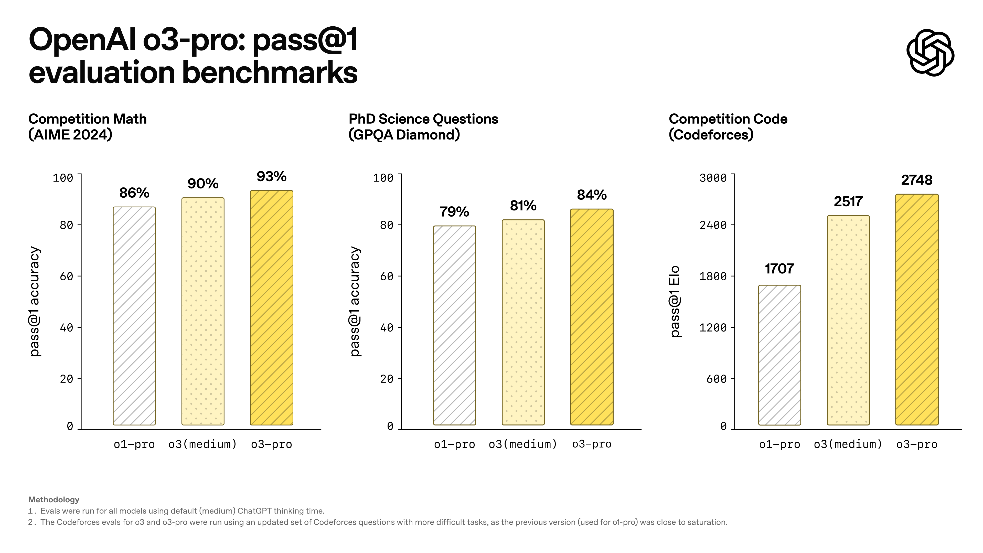
It’s quite cool both on benchmarks and according to human evaluation in the domains like science, education, programming, business, and writing help (don’t expect it to be a great creative writer though; it’s not created for that).
I wonder when it will become available for Plus tier :)
Meanwhile, OpenAI cut o3 prices by 80% and doubled rate limits for o3 for Plus users :O
WebDancer: Towards Autonomous Information Seeking Agency
https://arxiv.org/pdf/2505.22648
I’ve already shared in my reviews how curious I am about seeing attempts at training LLMs with RL in agentic environment, and recently I reviews the RAGEN paper, where LLMs were trained play games. But with WebDancer it’s getting more interesting, because its authors propose a framework for training LLMs for multi-turn information retrieval.
That’s like Deep Research, but complete agentic, structured in Thought-Action-Observation rounds, to the good ol’ traditions of ReACT:
- Observation contains planning process (long reasoning). Observations are enclosed in
... in the LLM’s generation. -
Action is one of the
search(query, filter_year),visit(goal, url_link),answer[which terminates the search process and returns the answer]. Search and visit actions are enclosed in<tool_call>...</tool_call>in the LLM’s generation, while the final answer comes as<answer>...</answer>. - Observation is:
- For a search action, the Top-10 titles and snippets,
- For a visit action, the evidence and an LLM-generated summary
Observations are put into prompts as
<tool_response>...</tool_response>segments.
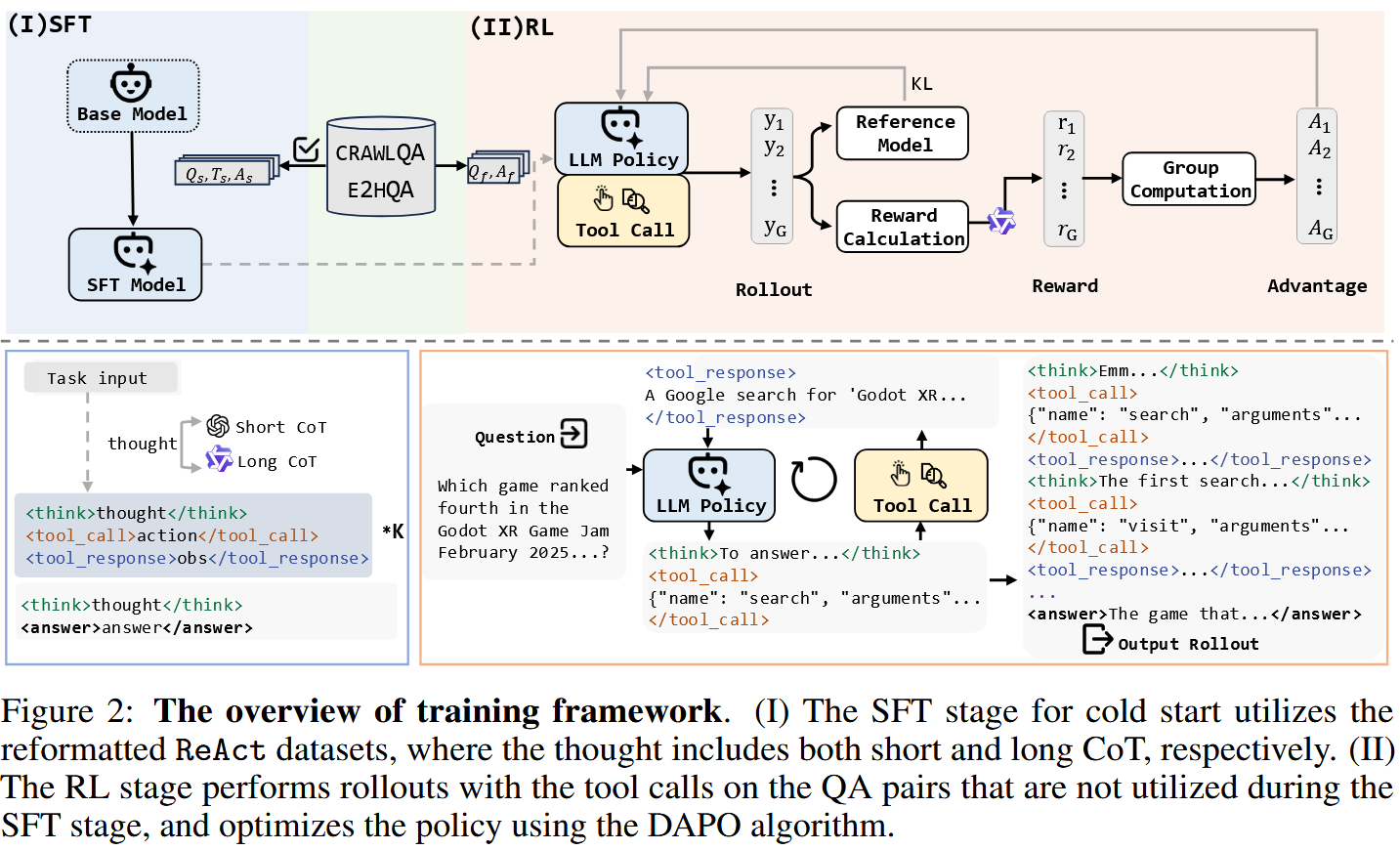
The authors train several Qwen models: Qwen-2.5-7B, Qwen-2.5-32B, QwQ-32B. The training process consists of two stages:
- Supervised Fine Tuning to adapt the format instruction following to agentic tasks and environments.
- RL to optimize the agent’s decision-making and generalization capabilities in real-world web environments. They use DAPO as the RL algorithm. The reward is
0.1 \cdot score_format + 0.9\cdot score_answer
where
-
score_formatrewards for obeying<think>...</think>,<tool_call>...</tool_call>format and for tool call consistency score_answerrewards for the correct answer; however, the authors had to employ an LLM-as-a-Judge for that.- As in previous works, observations (tool call returns) are masked from policy gradient to avoid introducing external signal into the system.
Before I move on to the training data composition, I’ll note that, of course, this is not the first case of RL training for the retrieval task. One of the examples is Search-R1. However, Search-R1 only has a query tool (so, no web site crawling); also, its training lacked the SFT stage, and there was no format reward (somehow prompting did all the job).
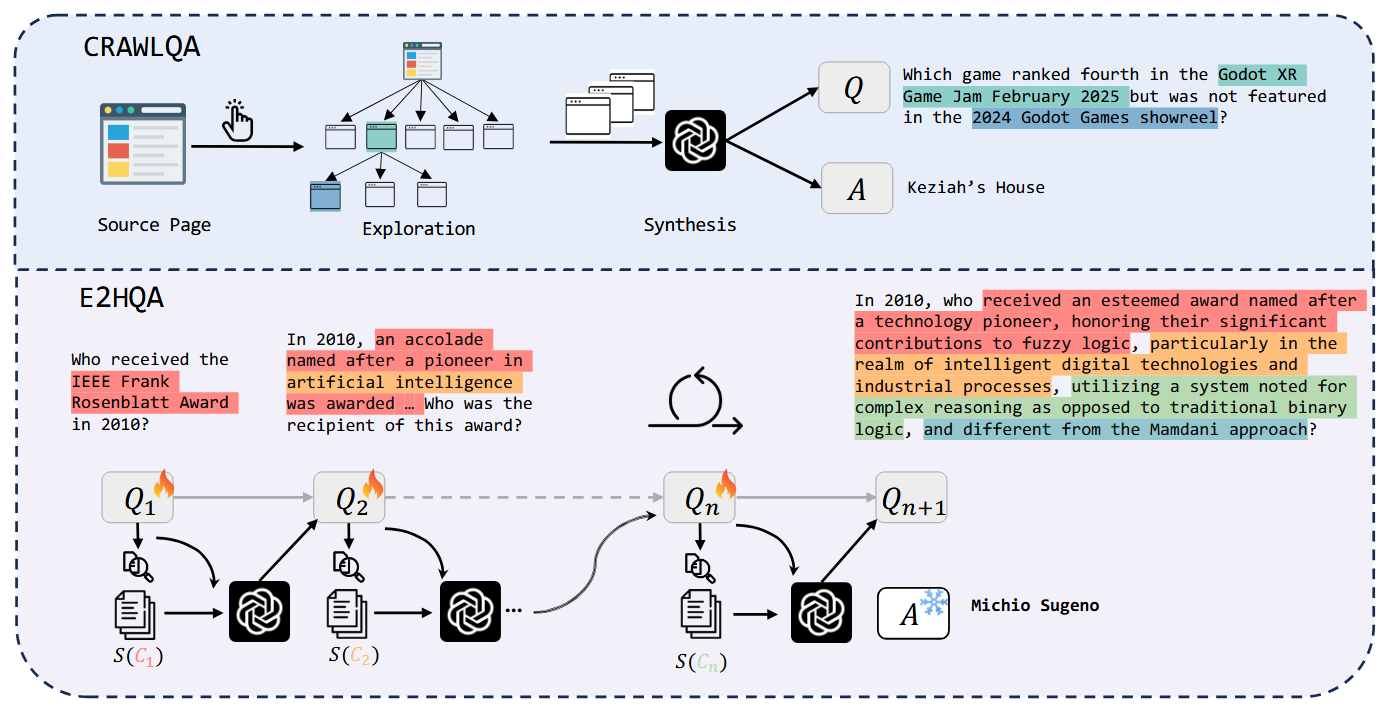
The authors collect two training datasets:
- CRAWLQA contains question-answer pairs synthesized by GPT-4o while exploring web sites.
-
E2HQA further refines this by rephrasing simple entities as their riddle-like explanations (see picture above). Then, the authors create agentic search trajectories, using two modes:
- Short CoT trajectories are just generated end-to-end by GPT-4o, each in one pass.
- Long CoT **trajectories are generated by QWQ-Plus (I’m not totally sure what the size of this model is; might be it’s also a 32B model, in which case we’ll be training QwQ-32B on correct trajectories of a comparable model) in real agentic interaction.
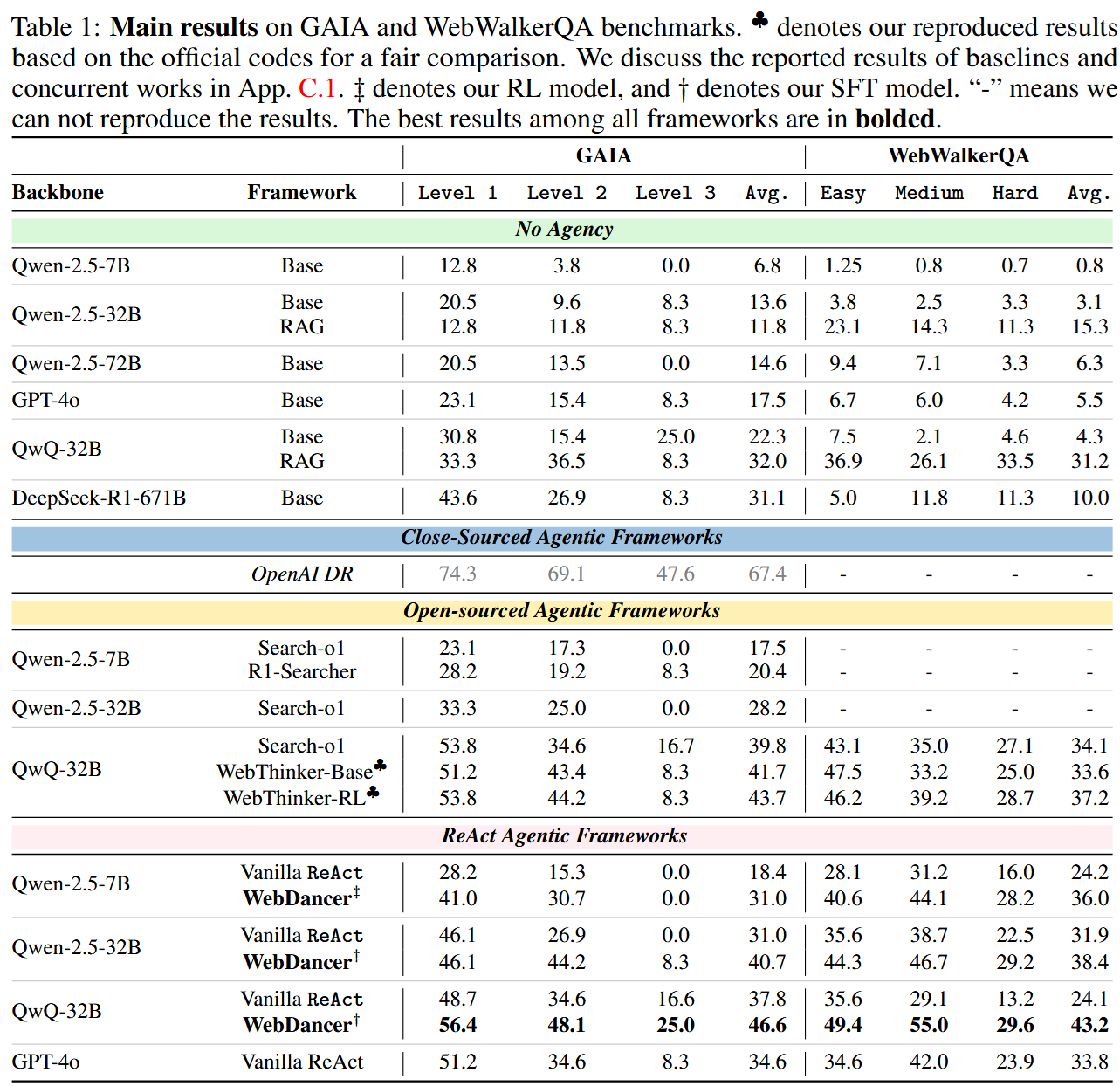
- The trajectories are further filtered based on their quality and correctness. Qwen-2.5-7B and Qwen-2.5-32B are only trained on Short CoT trajectories, while QwQ-32B is trained on long CoT. The results on GAIA and WebWalkerQA benchmarks are quite nice. The authors get significant improvement over Vanilla ReAct and previous framework such as R1-Searcher. In case of QWQ-32B it also beats GPT-4o acting in a ReAct way.
Darwin Gödel Machine: Open-Ended Evolution of Self-Improving Agents
https://arxiv.org/pdf/2505.22954
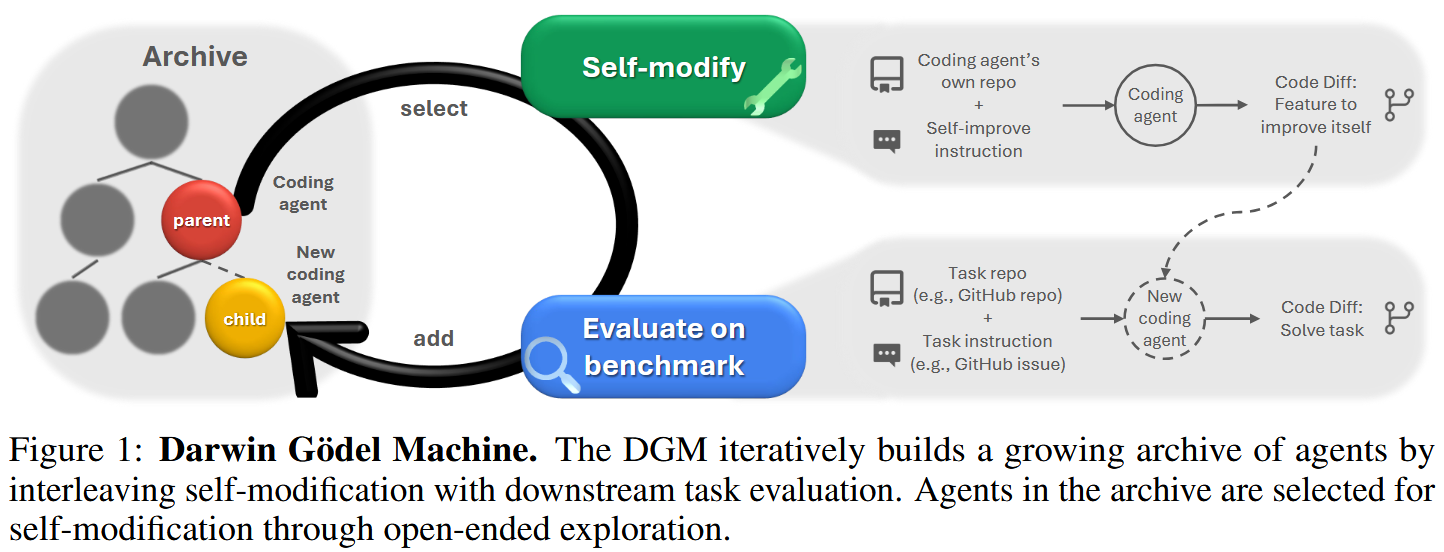
Why construct LLM agents if you can make them evolve and construct themselves? ;) The authors of this paper suggest something like MCTS in the world of agents. Starting from a simple coding agent with a bash tool and a file editing tool, the framework evolves new agents, balancing benchmark performance and novelty. Here is how they choose, on each step, k parent agent from the tree to produce new children:

(They use $k=2$ for SWE-bench and $k=4$ for Polyglot.) An important thing here is that these agents are capable of self-improvement. That is, when creating a new “child” agent, the “parent” agent analyses its benchmark logs and, based on this analysis, revises its own code, and prompt, and tools, and whatever, and it’s able to change them. (As opposed to a situation where modification is performed by an external, immutable agent.) At the same time, the LLM which powers the agent stays frozen.
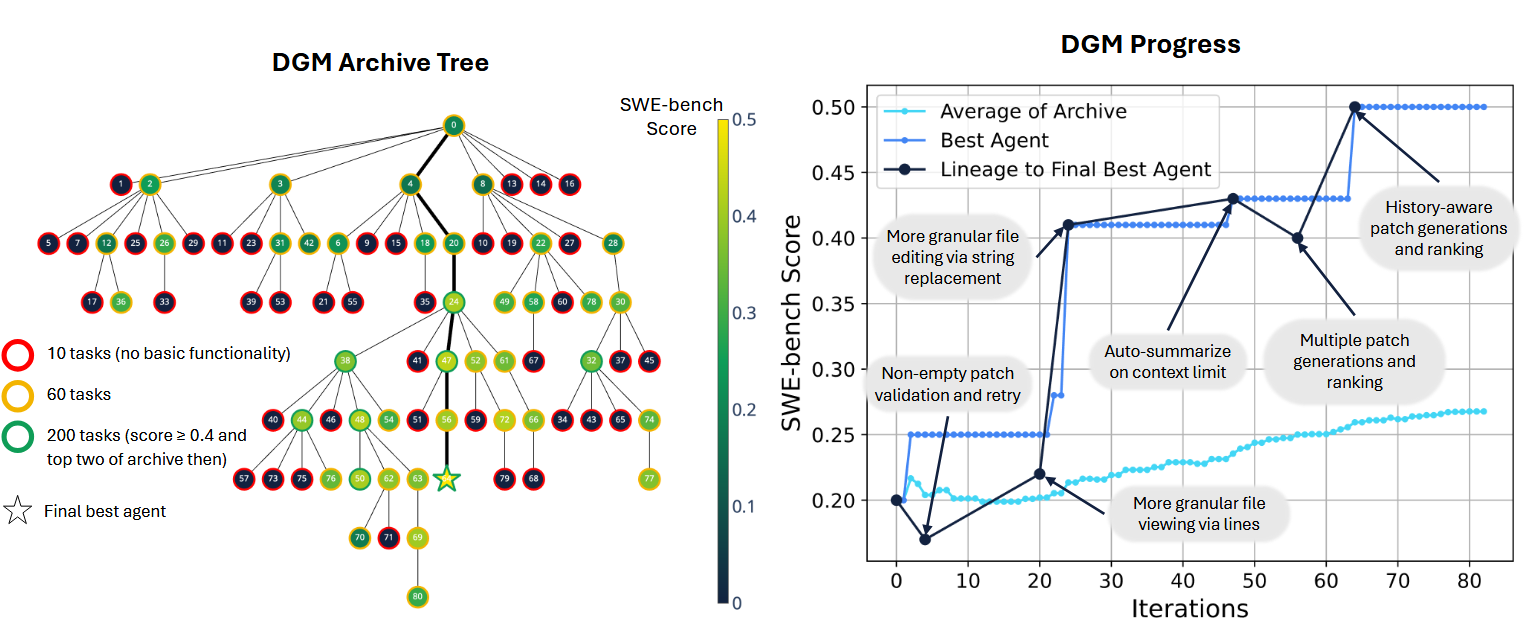
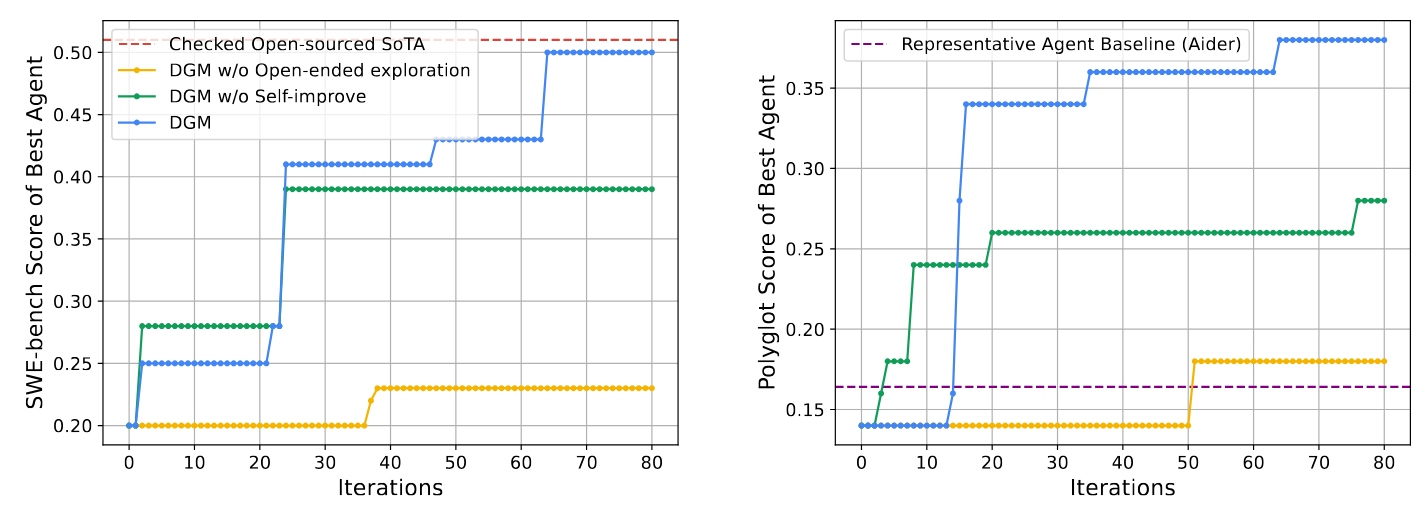
With this algorithm, the authors reach SoTA on SWE-bench for only USD 22,000. During self-modifications, coding agents are powered by Claude 3.5 Sonnet. During benchmark evaluation, coding agents are powered by Claude 3.5 Sonnet for SWE-bench and o3-mini for Polyglot. Ablation studies show the importance of both
- self-improvement - an agent modifies itself, so that the modification approaches also evolve, and
- open-endedness - quite confusingly, this refers to the tree search as opposed to sequential agent improvement. Well, indeed, tree search gives higher chances of avoiding local minima compared to sequential scenario.
Beyond the 80/20 Rule: High-Entropy Minority Tokens Drive Effective Reinforcement Learning for LLM Reasoning
https://arxiv.org/pdf/2506.01939
Non-linear LLM reasoning is quite an exciting thing to study. Of course, researchers mostly investigate its human-readable artifacts – all these “But wait”, “On the other hand”, “Alternatively” etc. In a sense, they build up a core long-reasoning toolset. But can we study this toolset without our a priori understanding of logical constructions – with math?
The authors of this paper start with something, which seems very different – from studying uncertainty of predicted token distribution. Let me explain it a bit. On each $i$-th generation step, and LLM predicts probabilities for every possible token to be the next one: $(p_{i,1},\ldots,p_{i,V})$, where $V$ is the vocabulary size. Now, this distribution might be more confident (the left example below) or less certain (the example on the right):
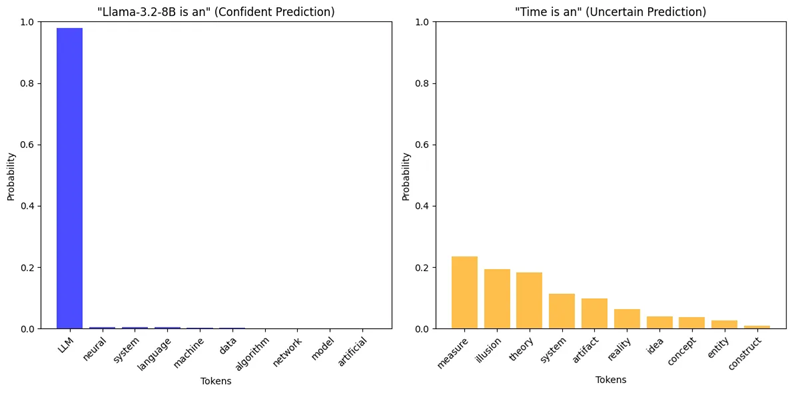
The level of uncertainty may be assessed by entropy:
\[H=-\sum_{v=1}^Vp_{i,v}\log{p_{i,v}}\]The higher the entropy, the less certain is the prediction.
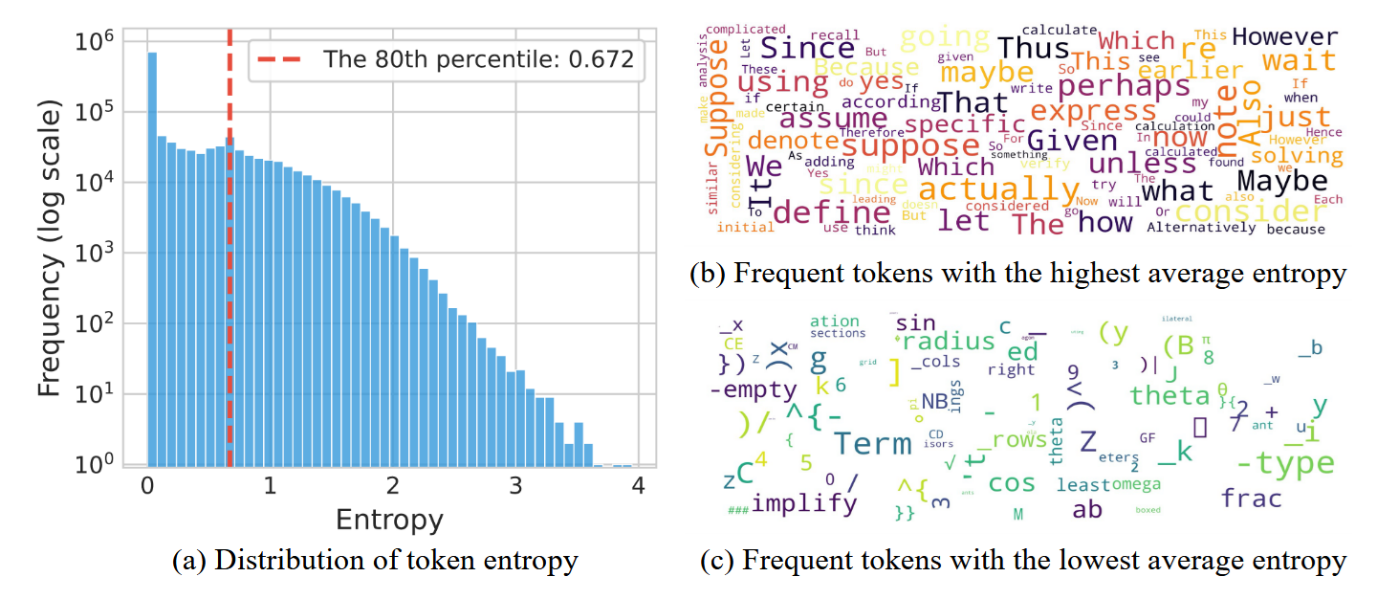
The authors run Qwen3-8B on queries from AIME’24 and AIME’25 (math Olympiad datasets), and they observed several curious things:
- Only about 20% tokens (i.e. positions in the sequence being generated) have relatively high entropy (that is, for these positions the LLM is quite uncertain about what to generate next).
- These tokens mostly correspond to reasoning cues such as “Since”, “Thus”, “Maybe” – and the familiar “Wait” am “Alternatively”. The authors characterize them as forks that lead to potential branching of reasoning, as opposed to in-branch tokens.
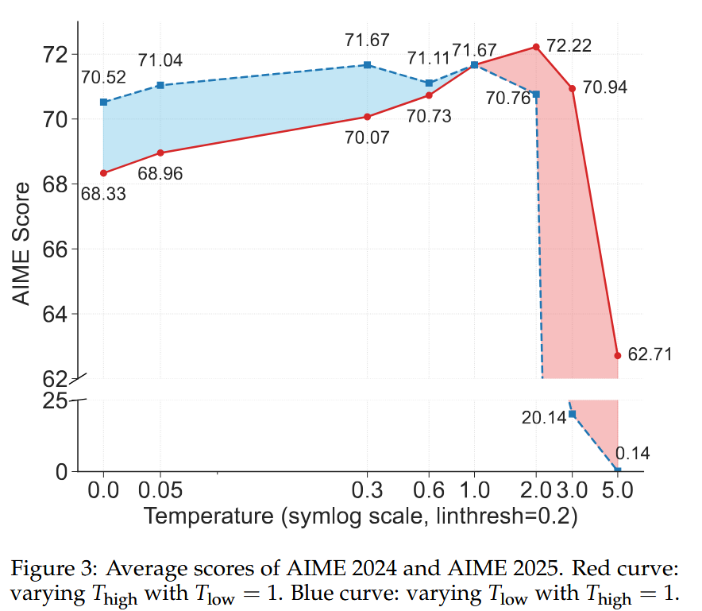
The authors perform an interesting experiment, varying generation temperature depending on the entropy:
\[p_{i}=\left(p_{i,1},…,p_{i,V}\right)=softmax\left(z_{i}/T_{i}^{'}\right)\]where
\[T_{i}^{'}=\left\{\begin{array}{c}T_{high},\text{ if }H_{i}>h_{threshold}\\T_{low},\text{ otherwise}\end{array}\right.\](Here $z_{i}$ are the logits and $H_{i}$ is the entropy of $softmax(z_{i})$, that is of probabilities generated under temperature $1.0$) Lowering $T_{high}$ makes generation at the corresponding steps more certain, and, as seen on the plot, it harms AIME score more severely than lowering $T_{low}$. On the other hand, as $T_{low}$ is increased (i.e. with generation at uncertain tokens becoming more uncertain), the quality degrades quite quickly.
This experiment seems to show that “fork” tokens really need to be high-entropy.
Leveraging fork tokens for improving RL training of long reasoners
The authors actually turn their theory into a nice practical application.
The most fashionable way of training non-linear reasoner LLMs is RL with accuracy/format rewards. Applying one of such techniques to Qwen3-14B, the authors discover that RL mostly alters entropies of tokens that already had high entropy:
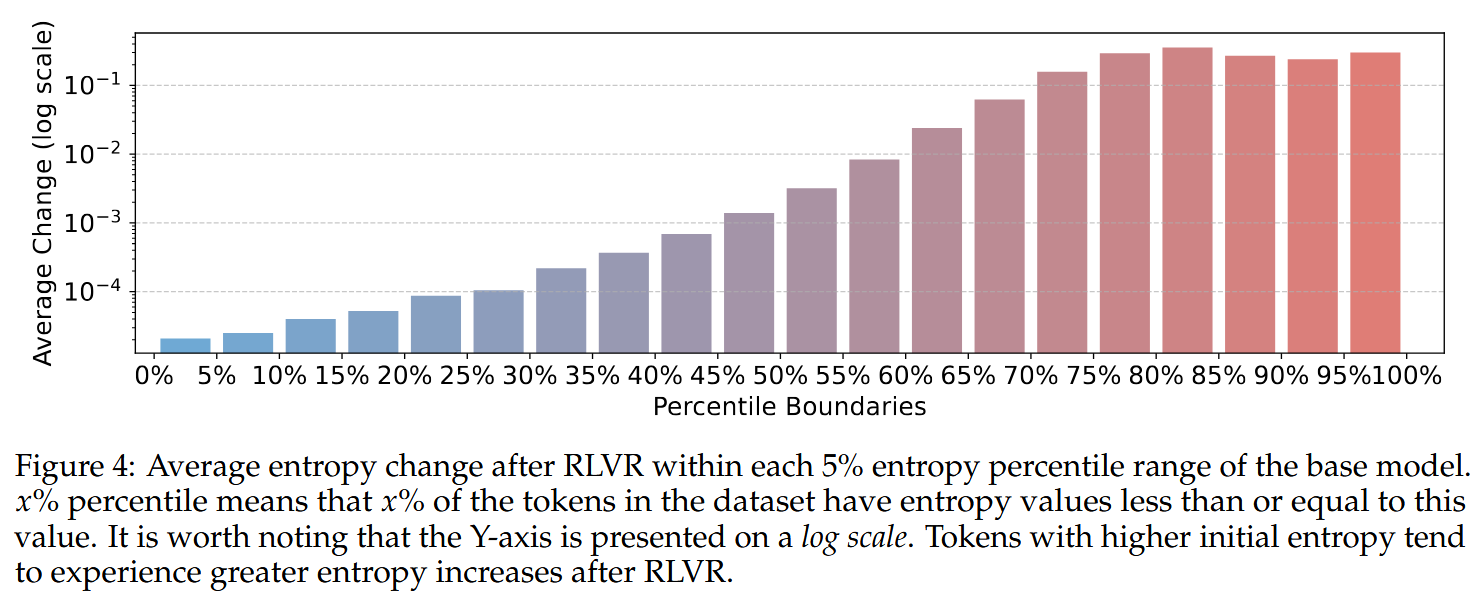
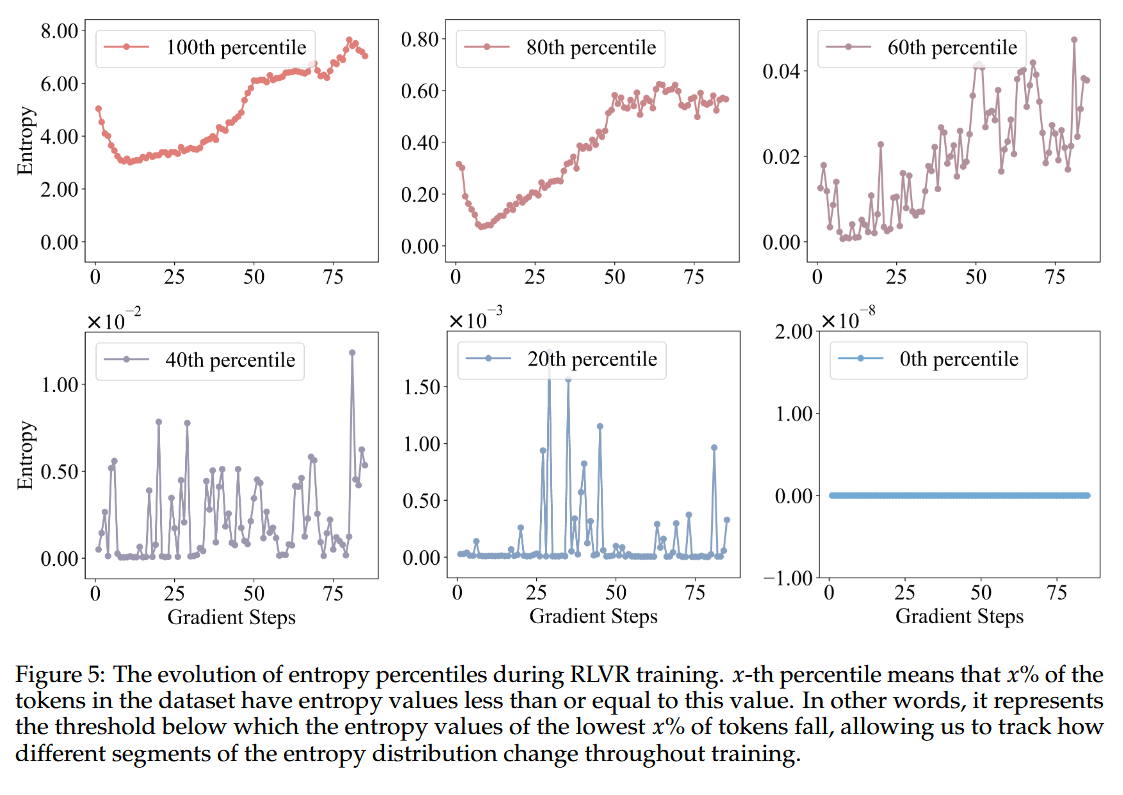
Now, the practical idea that the authors suggest for improving RL training is: let’s discard policy gradient of low-entropy tokens and only concentrate on high-entropy ones! This sounds like: let’s teach the LLM to use reasoning cues in a cool way, while disregarding whatever comes between them.
Mathematically it means the following changes in the loss:

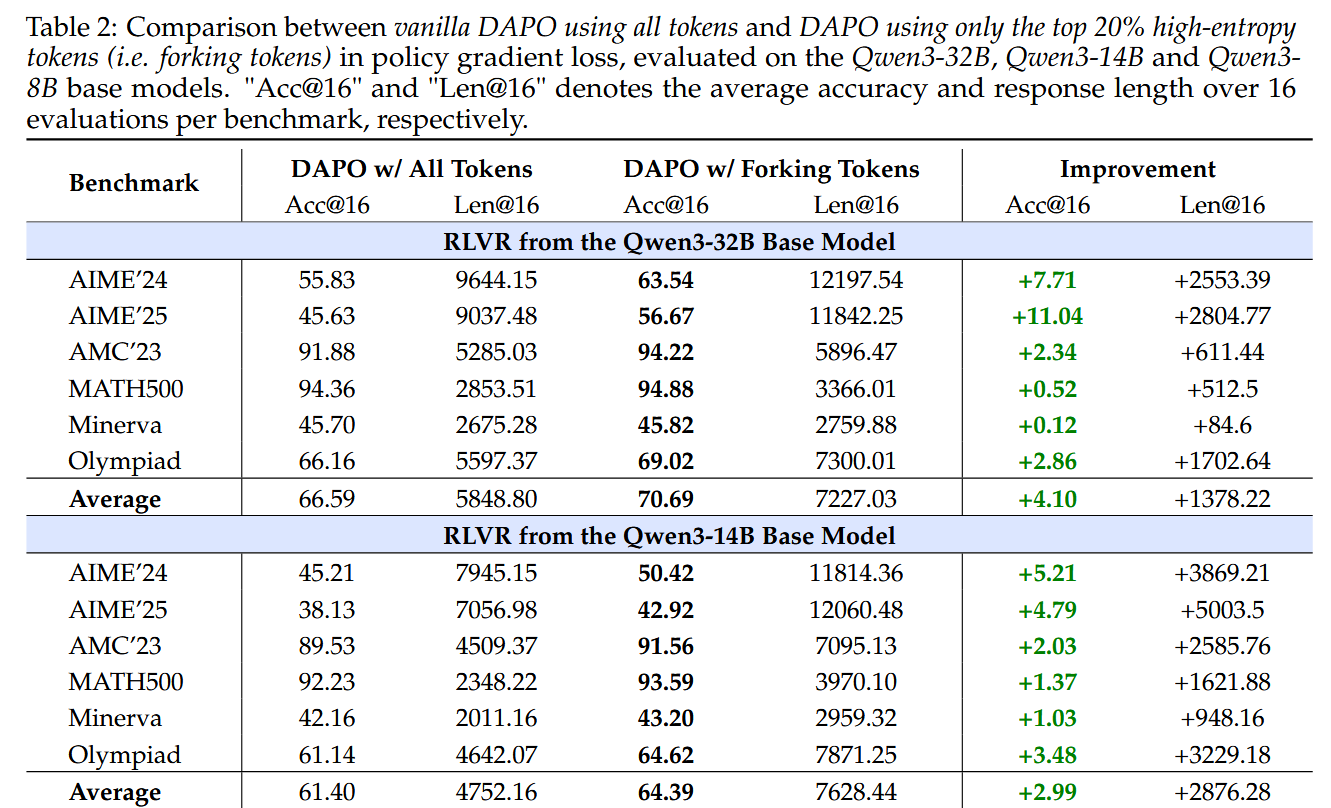
And here is a part of the table with results, showing some nice improvements for Qwen3-32B and Qwen3-14B models:
Spurious Rewards: Rethinking Training Signals in RLVR
In the previous paperwatch, we discussed the Unreasonable Effectiveness Of Reasonless Intermediate Tokens paper, which showed that by training an LLM on irrelevant reasoning traces, we can improve the final result. The authors of this paper investigate another crazy thing – RL training of a long reasoner with a completely broken reward model. They consider the following training regimes:
-
RL + format reward (reward responses with \boxed{})
- RL + incorrect reward (only incorrect answers rewarded)
- RL + random reward
- (as a reference) RL + correct ground-truth reward And here’s what they get on MATH-500:
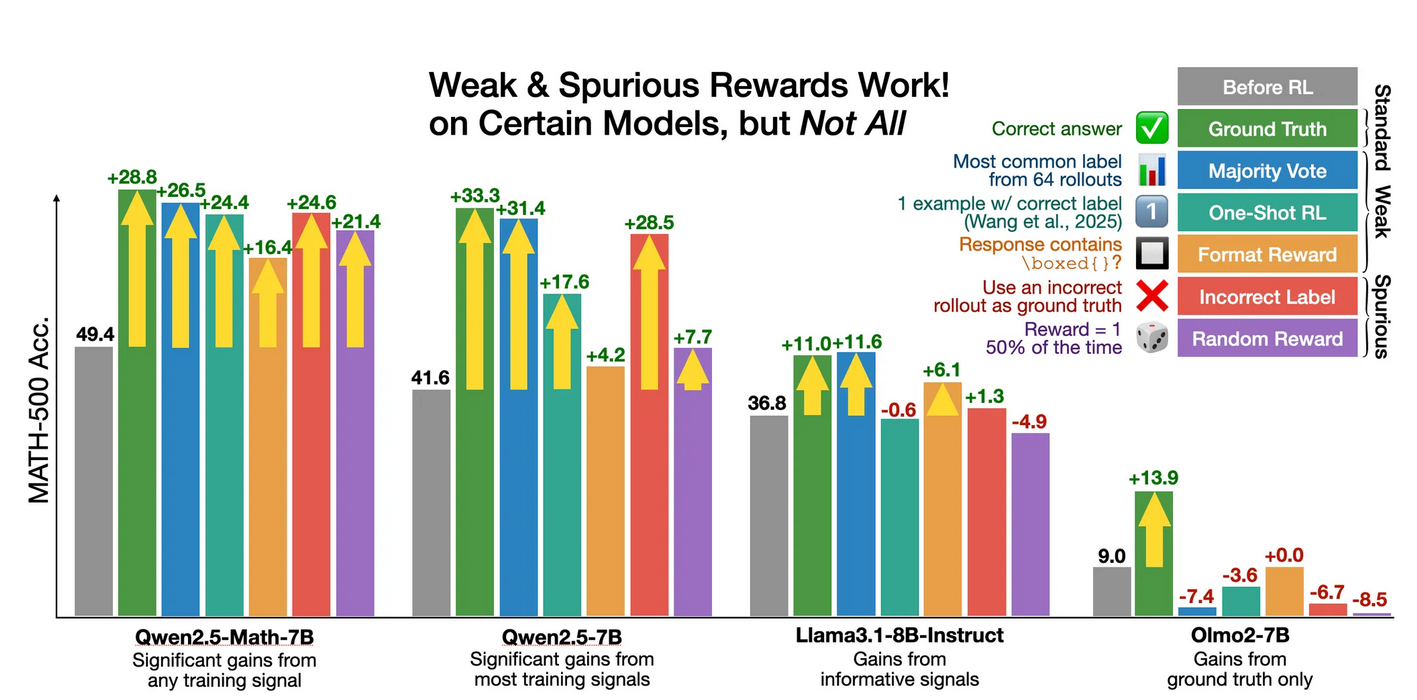
Sounds crazy!
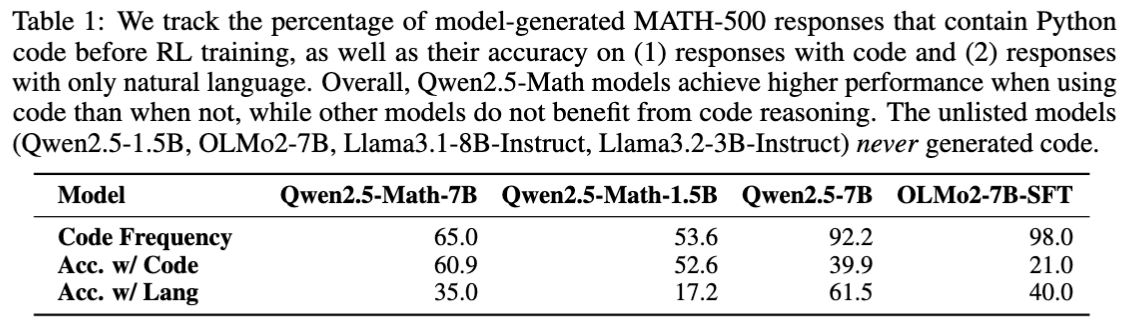
Of course, the authors tried to understand what happened and why Qwen-Math can be improved through training with incorrect rewards while other models can’t. They discovered that Qwen actively generates Python code to solve math problems, 65.0% of the time even before RL training (see the screenshot on the next page), and even though it doesn’t have access to a code interpreter. (So, it’s just generating output to its own code…) Moreover, there is a positive correlation between the amount of code and the correctness of its answers.
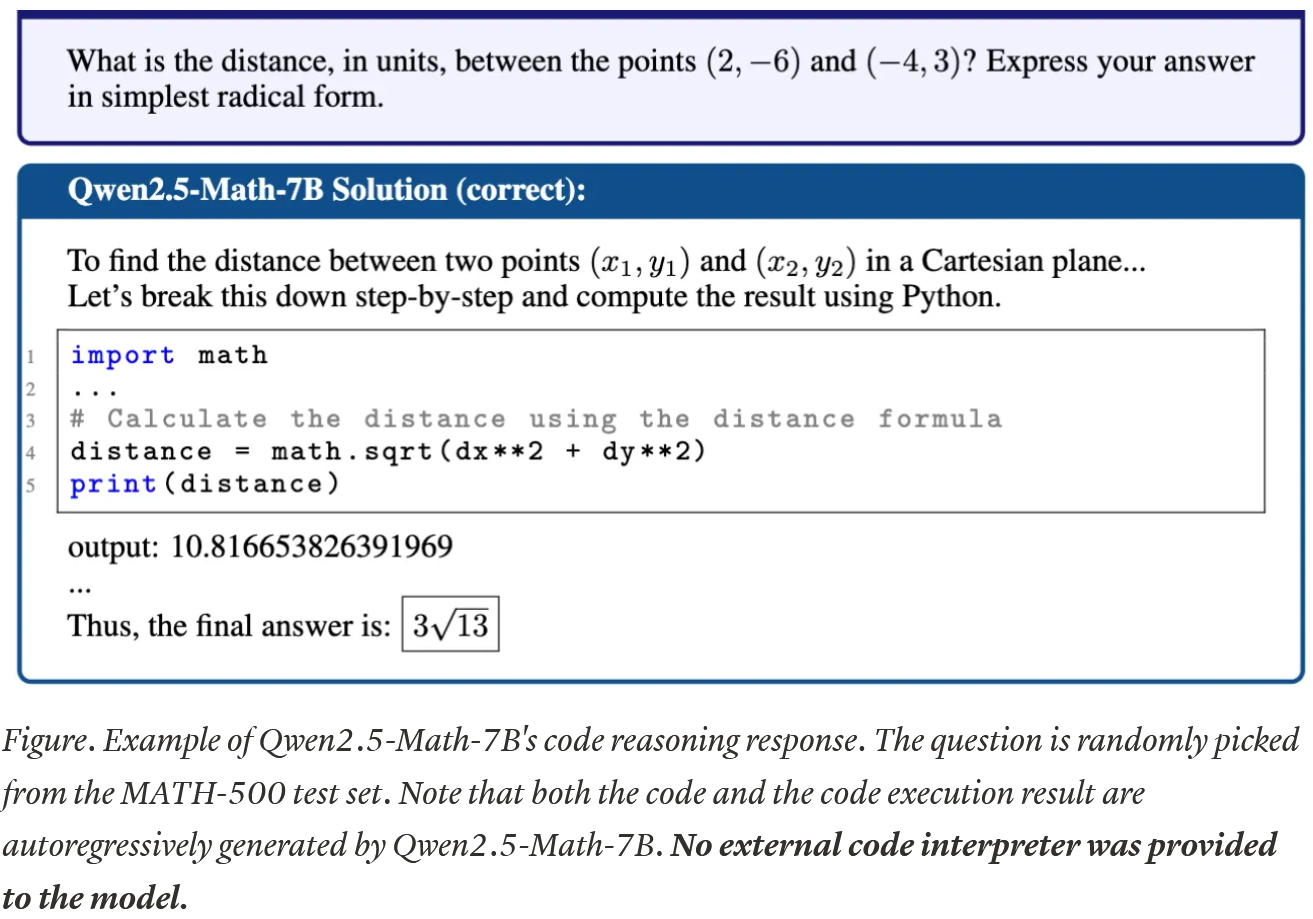
For other models, the situation is different: they either don’t generate code or they solve problems better without it.
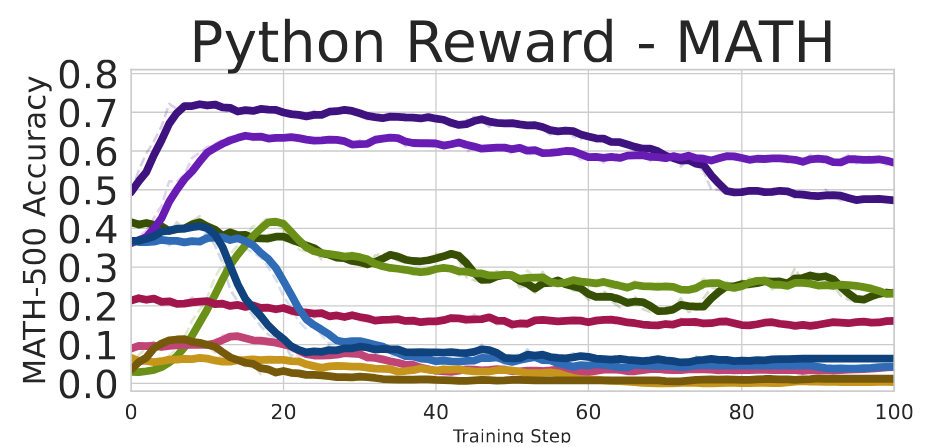
And it turns out that spurious rewards switch Qwen-Math quite aggressively into generating code: To check this, the authors train the models with a reward for the python substring, and, as expected, Qwen-Math models benefit from such training, while other models don’t:
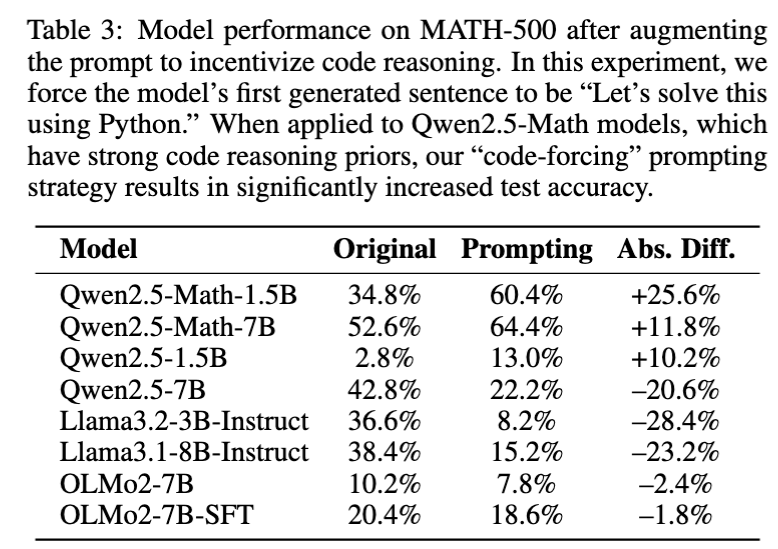
And then they just prompt the models to solve the problem using Python, discovering a similar pattern:
As for training with random rewards, the authors find out that the clipping in the GRPO loss seems to be the culprit, see this ablation study:
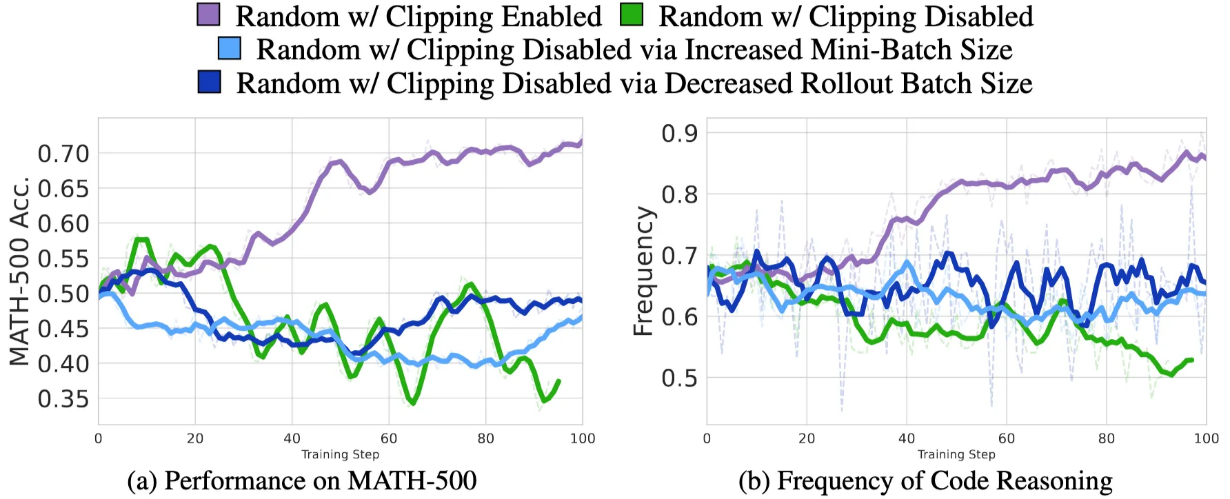
That’s not the first paper blaming clipping for various peculiarities of RL training. For example, DAPO suggested non-symmetric clipping to give low-probability, “exploration” tokens a chance to get a probability increase. Here’s the fix by DAPO (in red):
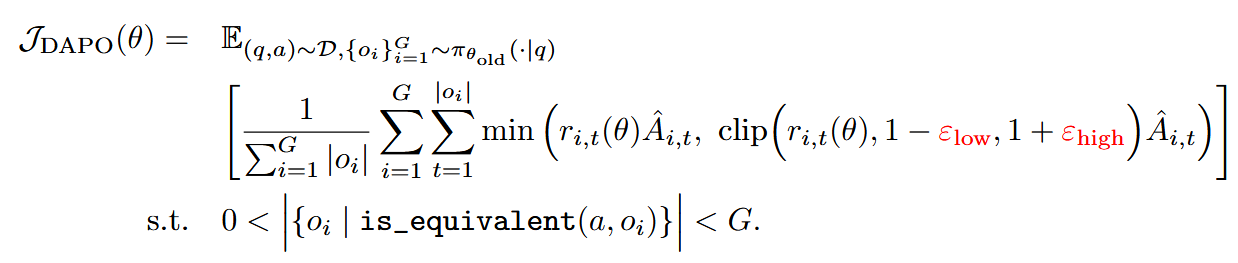
Here, the authors reiterate on this idea, explaining that clipping prevents low-probability samples from receiving substantial upweighting during training, causing the model to concentrate probability mass on its existing distribution. So, in absence of a reasonable reward signal, the model just reinforces its coding behaviour, which, curiously, leads to accuracy increase.
Learning to Reason without External Rewards
https://arxiv.org/pdf/2505.19590 And now that we’ve seen how spurious rewards work, let’s look if one can train a long reasoner without extrinsic rewards!
The authors of this paper suggest to use, instead of accuracy-based or format-based rewards, a model’s self-certainty – which is KL-divergence between the next-token distribution $p_{π_{θ}}(j\vert q, o<i)$ predicted by this model and the uniform distribution $U$ over the vocabulary:
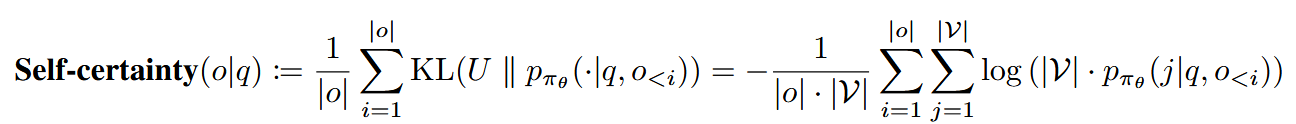
So, this reward drives the model away from uniformity, towards distribution modes (potentially reinforcing model’s distinctive patters – and I feel here something resonating with code-encouraging spurious rewards from the previous paper). The authors themselves argue that optimizing for self-certainty thus encourages the model to generate responses that it deems more convincing.
By the way, the authors already had experience of using self-certainty as proxy to correctness in their Scalable Best-of-N Selection via Self-Certainty paper.
The loss function itself is quite conservative:

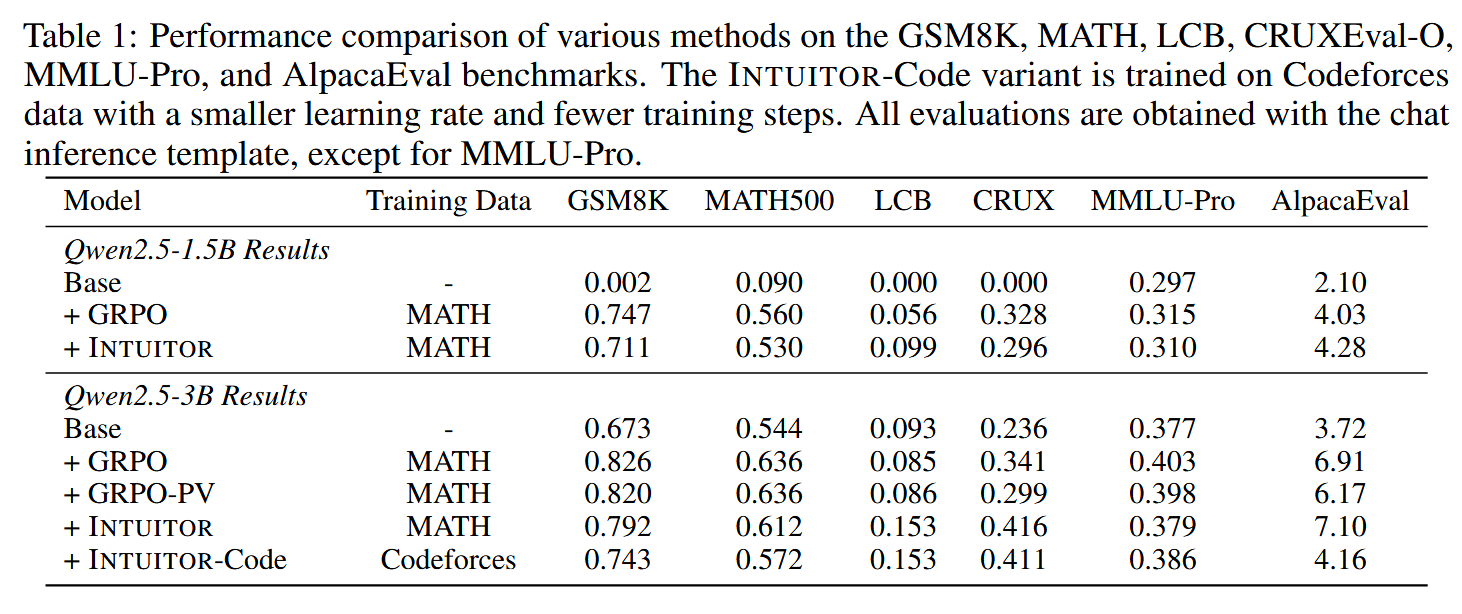
The approach, which the authors call INTUITOR, cannot beat GRPO, but approaches it, despite seemingly brining no information about ground truth:
From Tokens to Thoughts: How LLMs and Humans Trade Compression for Meaning
https://arxiv.org/pdf/2505.17117
This is a paper co-authored by Yann LeCun and Dan Jurafsky – should be interesting!
The authors apply information theory and psychological studies to answer three questions:
[RQ1]: To what extent do concepts emergent in LLMs align with human-defined conceptual categories?
[RQ2]: Do LLMs and humans exhibit similar internal geometric structures within these concepts, especially concerning item typicality?
[RQ3]: How do humans and LLMs differ in their strategies for balancing representational compression with the preservation of semantic fidelity when forming concepts? The authors approach these questions by analyzing concept clustering. They leveraged several influential psychological studies to gather a dataset of concepts such as ‘furniture’, ‘bird’, ‘fruit’, ‘clothing’, ‘robin’, ‘orange’, and ‘dress’. These concepts can be clustered
- For humans, using partition into semantic categories (for example, ‘robin’ falls in ‘bird’ category)
- For LLMs, concepts (i.e. corresponding words) are mapped to their embeddings and clustered with k-means
Of course, these clustering types are quite different. Now, with this clustering come two important concepts:
- Compression – how well we compress concepts in clusters/categories
- Distortion – relates to how much information is lost by compression The authors measure the efficiency of clustering of the initial concept dataset $X$ into clusters $C$ with the following loss:
where

-
Complexity is measured by the mutual information $I(X;C)$
\[\log_{2}|X|-\frac{1}{X}\sum_{c\in C}|C_{c}|log{|C_{c}|},\]where $C_{c}$ is the size of the $c$-th cluster. You can roughly understand this in the following way. Imagine that you need to find a particular concept in the total concept pile. If there are no clusters, you need $log_{2}\vert X\vert $ bits of information for that. Now, if someone tells you in which cluster the concept is, you might need like $\frac{1}{X}\sum_{c\in C}\vert C_{c}\vert log{\vert C_{c}\vert }$ bits of information to find it in this cluster. So, the difference between these two values shows smth how much knowing a concept’s cluster reduces the uncertainty of identifying that specific concept.
-
Distortion is measured by the weighted average of in-cluster variances:
Indeed, it represents how much geometrical information we lose if we replace every concept with the corresponding centroid.
Now, comparing cluster efficiency of clustering by humans ( = partition into categories) and LLMs gives the following insight into LLMs demonstrate markedly superior information-theoretic efficiency in their conceptual representations compared to human conceptual structures gives the following insight into [RQ3]:
- LLMs demonstrate markedly superior information-theoretic efficiency in their conceptual representations compared to human conceptual structures. That is, LLMs better balance complexity and distortion.
- To answer [RQ1], they calculate Adjusted Mutual Information (AMI) between human and LLMs’ clustering (AMI is 1 for identical partitions and 0 between independent random partitions). The takeaway is: Yes, there is above-chance alignment between concept clustering by humans and LLMs, and BERT is especially aligned, for some reason.
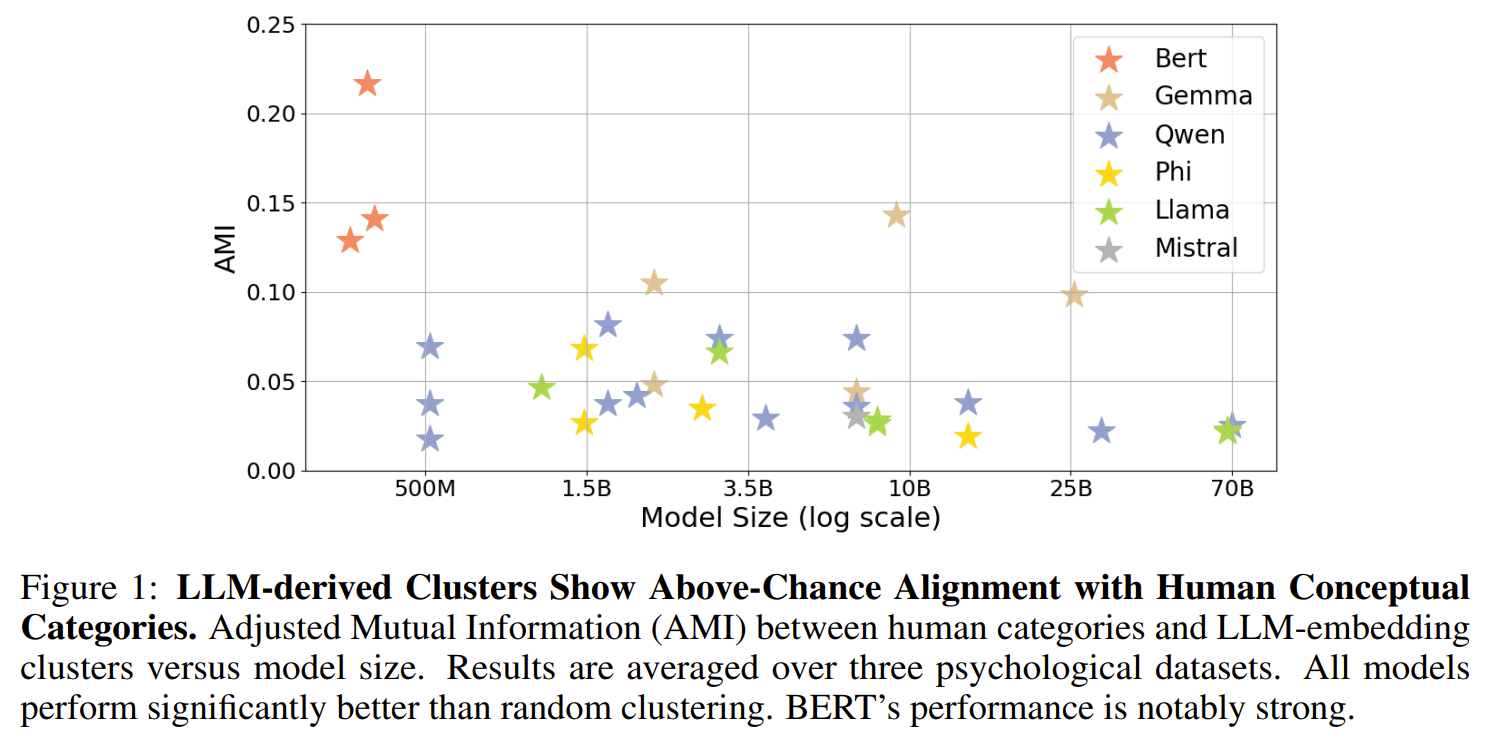
Finally, [RQ2] is about inner cluster structure, correspondence between metric vs psychological distance between concepts and category labels. (Like, ‘robin’ is a more typical representative of ‘bird’ category than ‘penguin’). Here, the finding is:
- Internal representations of LLMs demonstrate only modest alignment with human-perceived fine-grained semantic distinctions
Well, humans have strange ideas about various things; maybe, that’s why we compress concepts less efficiently :)
How much do language models memorize?
https://arxiv.org/pdf/2505.24832
This paper, which boasts authors from Meta, Google DeepMind, NVIDIA, and Cornell University, studies how much LLMs memorize. Why is it important? Well, there are at least two reasons:
- It helps to somehow map the amount of knowledge onto the amount of model parameters. (The previous attempt I remember was the Knowledge Capacity Scaling Laws paper, which predicted that LLMs can store 2 bits of knowledge per parameter.)
- It helps assess the trade off between memorization and generalization, which contributes to the “AGI is tomorrow” vs “LLMs are statistic parrots” discussion.
- Well, and it’s also relevant to the concerns about LLMs as copyright infringers :)
- And also it might help to understand whether it’s good to train models far past dataset sizes advised by scaling laws. (And it’s quite usual now to train LLMs on much, much data, disregarding the scaling laws.)
The paper opens with a math-heavy discussion of the concepts of memorization and unintended memorization, which we’ll largely omit, concentrating on the final results. Given a dataset $X$, a trained model $Θ$, and a reference model $Θ$ (for which the authors take a large model trained on much data, but not on $X$ in particular – a powerful generalist), we can define unintended memorization as
\[-\log{p(X|Θ)}+\log{\max(p(X|Θ), p(X|Θ))}\](At least this is how I understood the authors’ idea.)
The idea is the following:
- $-\log{p(X\vert Θ)}$ is a proxy for the amount of surprise that X can bring us compared to data generated by $Θ$. For example, a good fantasy novel will be quite surprising compared to quite repeating and bland fantasy-styled generations of any existing LLM. Also, a groundbreaking, Abel-prize-winning proof of a math theorem would be very surprising compared to math efforts of today’s LLMs, as well as compared to math efforts of most researcher.
Why is this a good proxy for the amount of surprise? Indeed, at the level of individual tokens,
- If $p(x\vert \widehat{\theta})$ is high, the token is predicted almost certainly, so there’s not much surprise
- If $p(x\vert \widehat{\theta})$ is low, the model is likely uncertain of its generation. (That’s not completely true, of course, but this is a good proxy.)
- $-\log{\max(p(X\vert \widehat{\theta}), p(X\vert \widehat{\theta}))}$ is the proxy for the amount information in $X$ that can’t be predicted by either a generalist ($Θ$) or specialist ($Θ$) model.
- The difference shows the reduction is surprise about the dataset’s unique information that comes from knowing the generalist model $Θ$. In a sense, it separates specific quirks of the datasets $X$ learnt by $Θ$ from the general knowledge learnt by both $Θ$ and $Θ$.
- Now that we understand a thing or two about what the authors measure, let’s look at some plots. The authors perform several experiments, including training on uniform random data and on real texts. The fun thing with real texts is that past some point, the unintended memorization actually starts to decrease, which the authors also relate to double descent and grokking. (And which, in my mind, is overcoming overfitting through dataset size.)
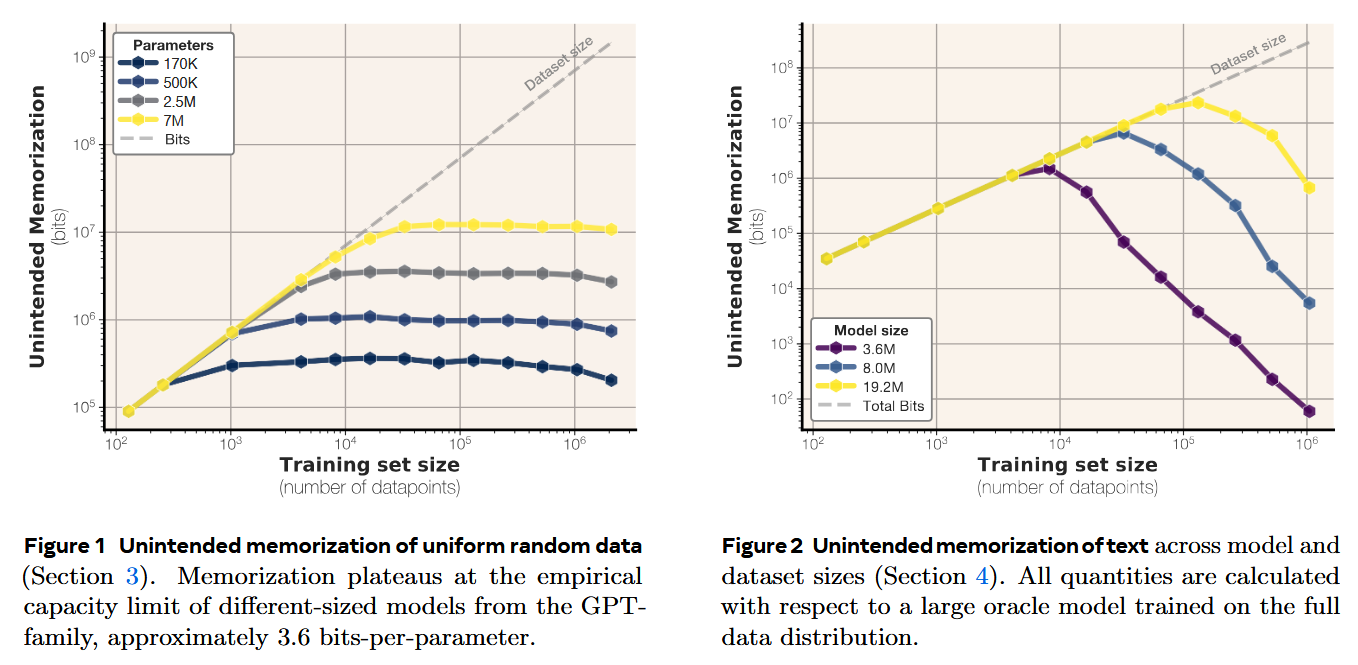
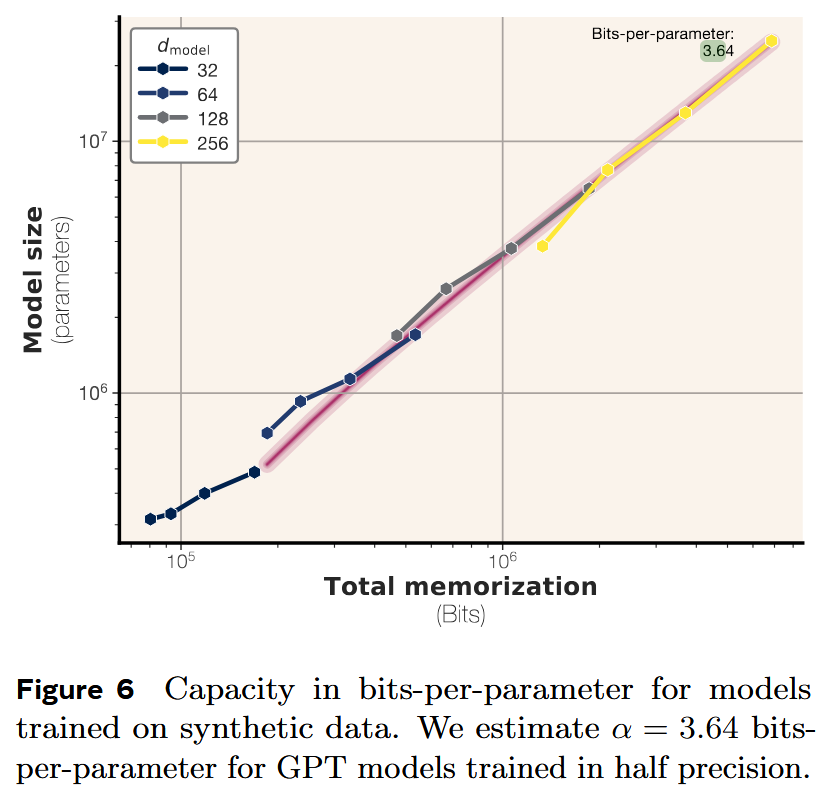
Also, they measure knowledge capacity (in bits per parameter) for the models they train – and here they train GPT-style models (like the good old times; think about GPT-2, not GPT-4o; why not Llama, I wonder) on random uniform data.
And find out that their capacity is 3.6 bits per parameter, which is more optimistic than 2 bits per parameter. That’s how many books per 7B model?:)
Beyond benchmark scores: Analyzing o3-mini’s mathematical reasoning
https://epoch.ai/gradient-updates/beyond-benchmark-scores-analysing-o3-mini-math-reasoning
Researchers from Epoch AI gathered 14 mathematician to analyze 29 of o3-mini-high’s raw, unsummarized reasoning traces on FrontierMath problems, which OpenAI shared with them. So, o3-mini-high got a bit of roasting :) And it’s curious to see which feats and problems real mathematician uncovered!
Here are some insights:
- The LLM is generally capable of understand the problem and fetching right theorems. (And no, mathematicians don’t think that o3-mini-high just memorized the right solutions and spat them out.)
- The LLM might be prone to somewhat informal reasoning, but on the other hand, it isn’t afraid of experimentation – quickly calculating something or writing some experimental code to progress in solving the problem. (Which is, in my mind, a good quality for a human mathematician.)
- The LLM sometimes makes a conjecture and just uses it without proving it – moving through pure guesswork. (Which is not too bad – many mathematicians have experience of drafting proofs with logic gaps that get filled afterwards.)
- The LLM might hallucinate, failing to accurately reproduce formulas. (I’m not surprised.) The verdict is that o3-mini-high as an “erudite vibes-based reasoner that lacks the creativity and formality of professional mathematicians, and tends to be strangely verbose or repetitive”. The authors also express concern about “why these models aren’t able to capitalize on this knowledge more substantially, making more connections between different subfields of math, creatively coming up with new ideas, and so on.”
And I’m thinking: are they supposed to? Of course, we don’t know how o3 is trained. So, let’s think about open-source long reasoners. They are usually trained with SFT on undergraduate-level tasks and RL with answer and format supervision – is it sufficient to produce really creative solutions that connect different branches of math? Or does such training produce a sneaky “student” who’s only concerned with getting the task solved, even if it requires a random guess? Maybe we need some other reward type or a different kind of training to awaken the LLM’s creative powers for math. It will be interesting to see some novel approaches.